二元函数

定义域

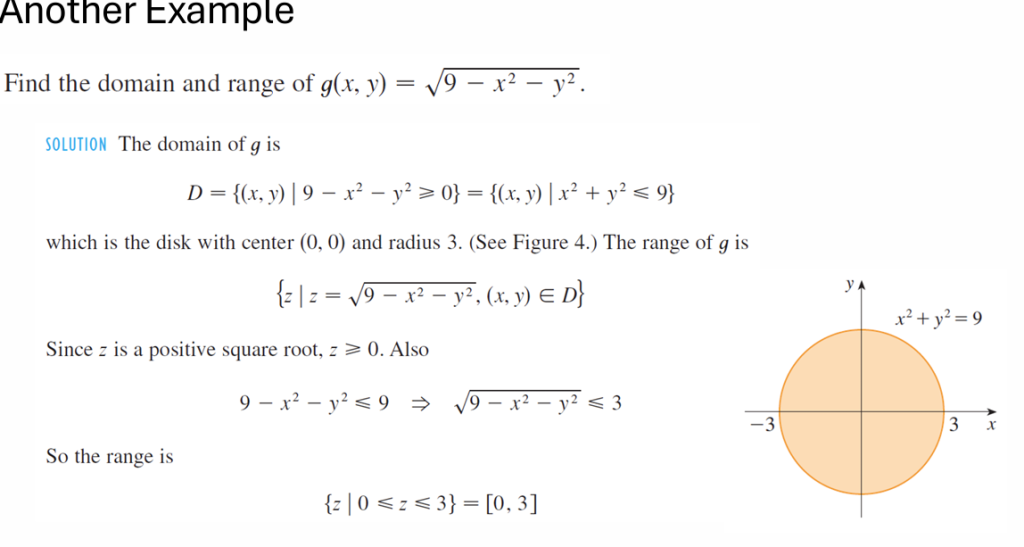
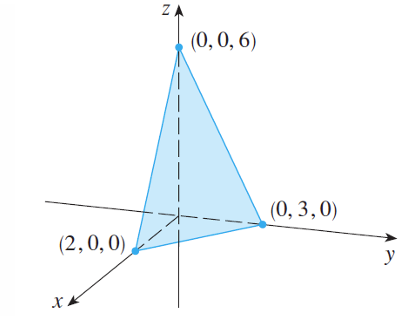
平面方程

常见二次曲面方程(补充)

最高次数为2的三元方程

球体方程

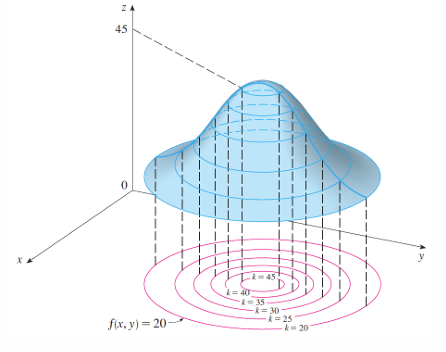
level Curves 等高线

二元函数 f 的等高线是方程 f(x,y)=k的曲线，其中 kk 为常数（属于 f的值域）。

等高线 f(x,y)=k 是定义域内所有使 f取值为 k的点的集合。换言之，它表示函数图像在高度 k 处的截面。

三元函数

level Surfaces 等值面

由于图像位于四维空间，三元函数 f的可视化非常困难。但通过观察其等值面(方程 f(x,y,z)=k的表面，k 为常数），我们可以获得一些理解。当点 (x,y,z)沿等值面移动时，函数值 f(x,y,z)保持不变

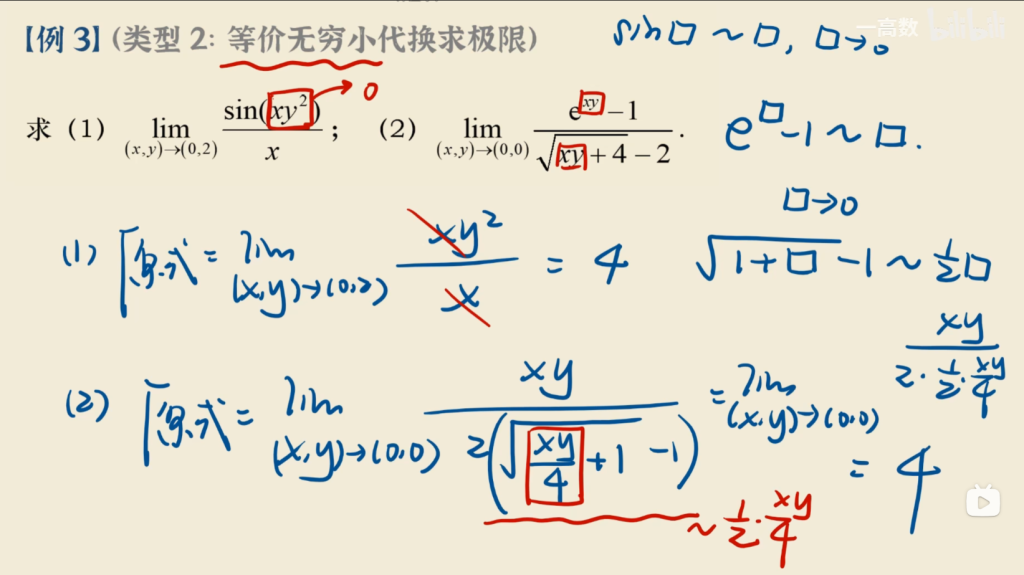
多元函数的极限

极限定义：

一元函数的极限，只有左/右逼近，二元及以上函数的极限可以从各个方向逼近，所以不能再用枚举法证明极限存在

例题：

如果存在极限

多元函数的连续性

连续：定义和一元相同，曲线某点连续的条件是极限与该点的函数值相同