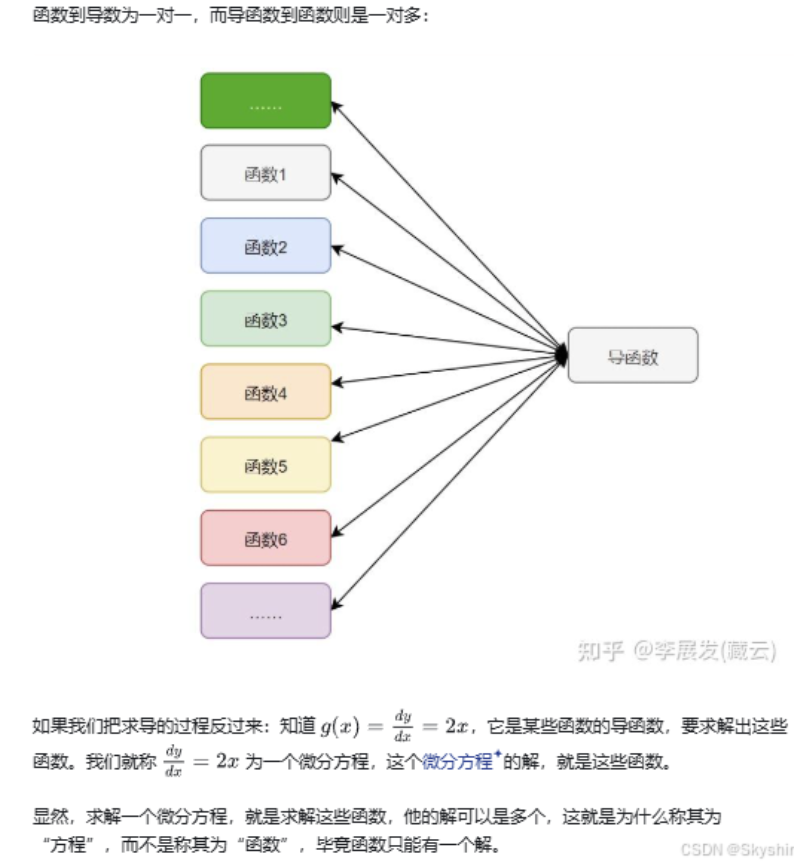
微分方程解法 Differential Equations solution

本文最后更新于3 天前，其中的信息可能已经过时，如有错误请留言

Differential Equation微分方程

微分方程：凡含有参数，未知函数和未知函数导数 (或微分) 的方程，称为微分方程，有时简称为方程，未知函数是一元函数的微分方程称作常微分方程，未知函数是多元函数的微分方程称作偏微分方程。微分方程中出现的未知函数最高阶导数的阶数，称为微分方程的阶(order)

Ordinary Differential Equation常微分方程(ODE)

若未知函数是一元函数的微分方程称为常微分方程。一般的 n 阶常微分方程的形式(也称隐式表达式)。可以看到全部都是一元函数的导数和自变量x，没有出现（xy）’的多元函数导数，注意一元函数可以是高幂的函数

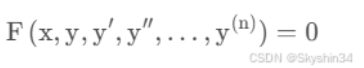
线性与齐次

Suppose that an ODE involves an unknown function $ y(x) $. Then the ODE is linear if it is one of the form:\[a_m(x) \frac{d^m y}{dx^m} + a_{m-1}(x) \frac{d^{m-1} y}{dx^{m-1}} + \ldots + a_1(x) \frac{dy}{dx} + a_0(x)y = f(x).\]

Any other type of ODE is nonlinear.

y及其各阶导数的最高次数为 1；
系数只能是关于自变量 x 的函数或常数（不能依赖于 y或其导数）变系数并不影响线性性，只要系数不依赖于y或其导数
不能有非线性函数（如 sin⁡(y)、$y^2$、$e^y$等）

$$-5 \frac{d^2 y}{dx^2} – 6 \frac{dy}{dx} + y = xe^x$$ 线性
$$-5 y \frac{d^2 y}{dx^2} – 6 \frac{dy}{dx} + y = xe^x$$ 非线性，y乘积
$$x^2 \frac{d^2 y}{dx^2} + x \frac{dy}{dx} + (x^2 – 1)y = 0$$ 线性，你可能误认为 (x2−1)y 的 y 是“系数”但实际上系数是 (x2−1)仅依赖于 x）
$$x^2 \frac{d^2 y}{dx^2} + x \left( \frac{dy}{dx} \right)^3 + (x^2 – 1)y = 0$$ 非线性，y有高次
$$x^2 \frac{d^2 y}{dx^2} + y \cos x = x^2$$ 线性，cosx 仅依赖于 x

齐次ODE：若f(x)=0，则为齐次ODE。
非齐次ODE：若f(x)≠0，则为非齐次ODE。

求解ODE的常用方法有分离变量法，如果是一阶ODE推荐积分因子法（通解公式）。当解析解难以或无法求得时，采用数值方法

问题建模：可分离变量微分方程

初始条件：8000 L 水中含 50 kg 盐，以 20 L/min 流入浓度 0.03 kg/L 的溶液，等速流出。目标：求 1 小时后剩余盐量。初始条件Define $ y(t) $ as the amount of salt in kilograms at time $ t $: $ y(0) = 50 $.

流入溶液的浓度为 0.03 kg/L，流速为 20 L/min，因此盐的流入速率为：\[
\text{流入速率} = 0.03\,\text{kg/L} \times 20\,\text{L/min} = 0.6\,\text{kg/min}
\]
流出速率：容器内混合溶液的体积恒为 8000 L，盐的浓度为 $\frac{y(t)}{8000}$ kg/L，注意此时盐浓度改变。流出速率为 20 L/min，因此盐的流出速率为：\[
\text{流出速率} = \frac{y(t)}{8000}\,\text{kg/L} \times 20\,\text{L/min} = \frac{y(t)}{400}\,\text{kg/min}
\]

\[\frac{dy}{dt} = 0.6 – \frac{y(t)}{400}\]

例2：

integrating factor 积分因子解一阶线性微分方程 – 通解公式

目标是将微分方程的一侧转化为某种形式，使其看起来像是乘积法则的求导结果。为此，我们需要将方程乘以一个精心选择的关于 x 的函数。这个函数称为积分因子，之后只需要两侧进行积分就可以解微分方程

求解微分方程：

\[ x \frac{dy}{dx} + 2y = e^x, \]

初始条件为 $ y(1) = 1 $。

首先将方程化为标准形式：

\[ \frac{dy}{dx} + \frac{2y}{x} = \frac{e^x}{x}. \]

因此 $ P(x) = \frac{2}{x} $。积分因子为：

\[ \lambda(x) = \exp\left(\int\frac{2}{x} dx\right) = \exp(2\ln|x|) = (e^{\ln|x|})^2 = |x|^2 = x^2. \]

将方程乘以 $ x^2 $，得到：

\[ x^2 \frac{dy}{dx} + 2xy = xe^x \]

可以表示为：

\[ \frac{d}{dx}(x^2y) = xe^x. \]

积分得到：

\[ x^2y = \int xe^x dx + C. \]

通过分部积分计算积分：设 $ f(x) = x $，$ g'(x) = e^x $，则 $ f'(x) = 1 $，$ g(x) = e^x $。因此：

\[ \int xe^x dx = xe^x – \int e^x dx = xe^x – e^x + A = (x-1)e^x + A. \]

因此，通解为：

\[ y = \frac{x-1}{x^2} e^x + \frac{C}{x^2}, \]

其中 $ x \neq 0 $。

根据初始条件 $ y(1) = 1 $，代入得 $ C = 1 $。

最终解为：

\[ y = \frac{x-1}{x^2} e^x + \frac{1}{x^2}. \]