DISTANCE FORMULA IN THREE DIMENSIONS
The distance \(|P_1 P_2|\) between the points \(P_1(x_1, y_1, z_1)\) and \(P_2(x_2, y_2, z_2)\) is
\[
|P_1 P_2| = \sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2 + (z_2 – z_1)^2}
\]
EQUATION OF A SPHERE with center \(C(h, k, l)\) and radius r
\[
(x – h)^2 + (y – k)^2 + (z – l)^2 = r^2
\]In particular, if the center is the origin O, then an equation of the sphere is
\[
x^2 + y^2 + z^2 = r^2
\]
例题:Show that \( x^2 + y^2 + z^2 + 4x – 6y + 2z + 6 = 0 \) is the equation of a sphere, and find its center and radius.
\[
(x^{2} + 4x + 4) + (y^{2} – 6y + 9) + (z^{2} + 2z + 1) = -6 + 14
\]\[
(x + 2)^{2} + (y – 3)^{2} + (z + 1)^{2} = 8
\]\[
\text{Centre } (-2, 3, -1), \text{ radius: } \sqrt{8} = 2\sqrt{2}
\]
\(\overrightarrow{P_1P_2}\) is a vector in 3-space with initial point \(P_1(x_1, y_1, z_1)\) and terminal point \(P_2(x_2, y_2, z_2)\), then
\[
\overrightarrow{P_1P_2} = \langle x_2 – x_1, y_2 – y_1, z_2 – z_1 \rangle
\]
NORM OF A VECTOR
For a 2D vector \(\mathbf{v} = (v_1, v_2)\):
\[
\|\mathbf{v}\| = \sqrt{v_1^2 + v_2^2}
\]
For a 3D vector $\mathbf{v} = (v_1, v_2, v_3)$:
\[
\|\mathbf{v}\| = \sqrt{v_1^2 + v_2^2 + v_3^2}
\]
DEFINITION OF THE DOT PRODUCT
If \(\mathbf{u} = \langle u_1, u_2 \rangle\) and \(\mathbf{v} = \langle v_1, v_2 \rangle\) are vectors in 2-space, then the dot product of u and v is written as \(\mathbf{u} \cdot \mathbf{v}\) and is defined as
\[
\mathbf{u} \cdot \mathbf{v} = u_1 v_1 + u_2 v_2
\]
vectors in 3-space, then their dot product is defined as
\[
\mathbf{u} \cdot \mathbf{v} = u_1 v_1 + u_2 v_2 + u_3 v_3
\]
例:
(3, 5) · (-1, 2) = 3×(-1) + 5×2 = -3 + 10 = 7
(3i + 5j) · (-i + 2j) = 3×(-1) + 5×2 = -3 + 10 =

Determinant

Cross Product 叉积
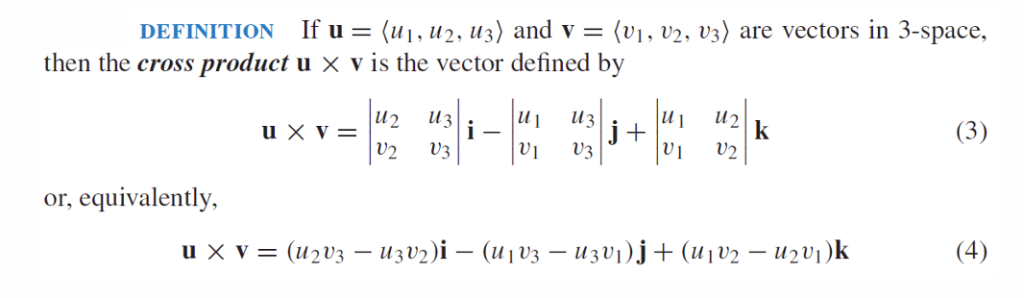
- 叉积只定义在三维空间,点击定义在二维和三维空间中
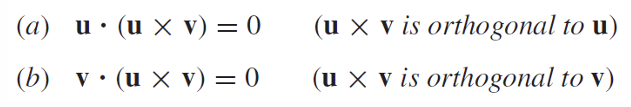
Scalar Triple Products 混合积

证明:

例1:
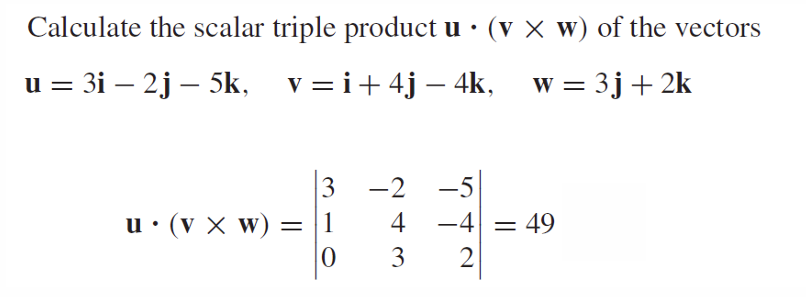
几何性质:

点和方向向量确定的直线参数方程

例:

例1:

例2:

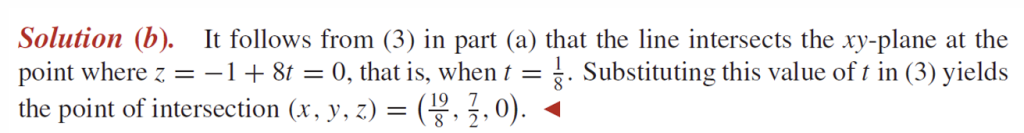
t1 = t2 + 1是因为直线的参数方程有不同的t与系数线性组合方式,3式如果让t1等于0与4式t2 = -1的X结果相同,由此可知,两个表示同一直线的参数方程的参数t1,t2之间的关系
例3:
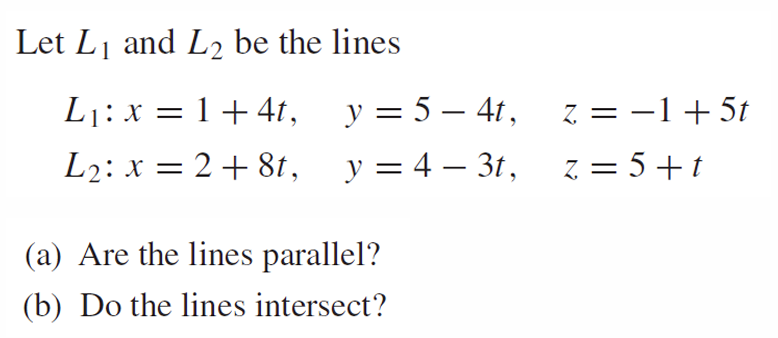

直线参数方程的向量表示:

由点及法向量确定的平面
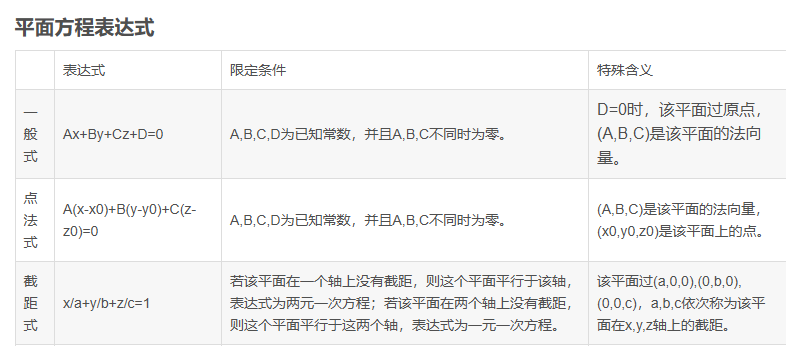
点法式:、(x-x0,y-y0,z-z0)平面内任意过点P0的向量与平面法向量(A,B,C)的向量积(数量积)为0
例: