Reference:如何简单理解概率分布函数和概率密度函数?_概率密度函数和分布函数的关系-CSDN博客https://blog.csdn.net/ypp0229/article/details/104982664
离散型随机变量和连续性随机变量
离散型随机变量是指其数值只能用自然数或整数单位计算的则为离散变量。例如,企业个数,职工人数,设备台数等,只能按计量单位数计数,这种变量的数值一般用计数方法取得。反之,在一定区间内可以任意取值的变量叫连续变量,其数值是连续不断的,相邻两个数值可作无限分割,即可取无限个数值。例如,生产零件的规格尺寸,人体测量的身高,体重,胸围等为连续变量,其数值只能用测量或计量的方法取得
离散型随机变量的概率函数 – 概率质量函数
与下面的连续随机变量的概率密度函数(PDF)不同,PMF直接给出了随机变量取某个值的概率。

离散型随机变量的概率分布
这样的列表都被叫做离散型随机变量的“概率分布”。严格来说,它应该叫离散型随机变量的值分布和值的概率分布列表”,这个名字虽然比“概率分布”长了点,但是肯定好理解了很多。因为这个列表,上面是值,下面是这个取值相应取到的概率,而且这个列表把所有可能出现的情况全部都列出来了!

离散/连续随机变量的(概率)分布函数 – 累积概率函数
设离散型随机变量X的分布律是
\[ P \{ X = x_k \} = p_k \quad k=1,2,3\cdots \]
则\[ F(x) = P(X \leq x) = \sum_{x_k \leq x} p_k \]F(x)就代表概率分布函数啦。即F(x)=P(X<x) (-∞<x<+∞)。这个符号的右边是一个长的很像概率函数的公式,但是其中的等号变成了小于等于号的公式。它就是概率函数取值的累加结果!所以它又叫累积概率函数!研究一个随机变量X取值小于某一数值x的概率,这概率是x的函数,称这种函数为随机变量ξ的分布函数简称分布函数
概率函数和概率分布函数就像是一个硬币的两面,它们都只是描述概率的不同手段!
于是连续型随机变量X的概率分布函数可写为常用的概率积分公式的形式:
\[F(x) = \int_{-\infty}^{x} f(x) \, dx.\]
连续随机变量的概率函数 – 概率密度函数
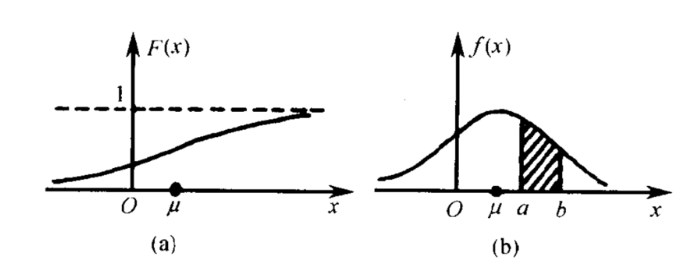
左边是F(x)连续型随机变量分布函数画出的图形,右边是f(x)连续型随机变量的概率密度函数画出的图像
连续型随机变量的“概率函数”换了一个名字,叫做“概率密度函数”,概率密度函数是分布函数的导函数。两张图一对比,你就会发现,如果用右图中的面积来表示概率,利用图形就能很清楚的看出,哪些取值的概率更大!所以,我们在表示连续型随机变量的概率时,用f(x)概率密度函数来表示,是非常好的!
定义为\( F_X(x) = \int_{-\infty}^{x} f_X(t) \, dt \),则 \( X \) 是一个连续型随机变量,并且 \( f_X(x) \) 是它的概率密度函数
概率质量函数 Vs. 概率密度函数
在概率论中,概率质量函数(probability mass function,简写为pmf)是离散随机变量在各特定取值上的概率。概率质量函数和概率密度函数不同之处在于:概率质量函数是对离散随机变量定义的,本身代表该值的概率;概率密度函数是对连续随机变量定义的,本身不是概率,只有对连续随机变量的概率密度函数在某区间内进行积分后才是概率。
逻辑回归

通过sigmoid函数将线性回归的结果映射到概率(0和1之间)
设 \( X \) 是连续随机变量,\( X \) 服从逻辑斯谛分布,则 \( X \) 具有下列分布函数和密度函数: \[ F(x) = P(X \leq x) = \frac{1}{1 + e^{-(x – \mu)/\gamma}} \tag{6.1} \] \[ f(x) = F'(x) = \frac{e^{-(x – \mu)/\gamma}}{\gamma (1 + e^{-(x – \mu)/\gamma})^2} \tag{6.2} \] 式中,\(\mu\) 为位置参数,\(\gamma > 0\) 为形状参数。

该曲线以点(\(\mu\),1/2)为中心对称
曲线表示基于条件,得出结果的概率,而如果要根据这些概率以0.5为界进行分类,则为逻辑回归模型
二项逻辑回归模型
虽然叫做逻辑回归,但实际是分类模型
对于给定的输入实例 \( x \),按照式 (6.3) 和式 (6.4) 可以求得 \( P(Y = 1|x) \) 和 \( P(Y = 0|x) \)。逻辑斯谛回归比较两个条件概率值的大小,将实例 \( x \) 分到概率值较大的那一类。
有时为了方便,将权值向量和输入向量加以扩充,仍记作 \( w \),\( x \),即
\[
w = (w^{(1)}, w^{(2)}, \cdots, w^{(n)}, b)^T, \quad
x = (x^{(1)}, x^{(2)}, \cdots, x^{(n)}, 1)^T.
\]
这时,逻辑斯谛回归模型如下:
\[
P(Y = 1|x) = \frac{\exp(w \cdot x)}{1 + \exp(w \cdot x)} \tag{6.5}
\]
\[
P(Y = 0|x) = \frac{1}{1 + \exp(w \cdot x)} \tag{6.6}
\]
这里,\( x \in \mathbb{R}^n \) 是输入,\( Y \in \{0,1\} \) 是输出,\( w \in \mathbb{R}^n \) 和 \( b \in \mathbb{R} \) 是参数,\( w \) 称为权值向量,\( b \) 称为偏置,\( w \cdot x \) 为 \( w \) 和 \( x \) 的内积。
一个事件的几率(odds)是指该事件发生的概率与该事件不发生的概率的比值(概率是发生的概率 / 所有可能的概率和)。如果事件发生的概率是 \( p \),那么该事件的几率是
\[
\frac{p}{1-p},
\]
该事件的对数几率(log odds)或 logit 函数是
\[
\mathrm{logit}(p) = \log \frac{p}{1-p}.
\]
对逻辑斯谛回归而言,由式(6.5)与式(6.6)得 \[ \log \frac{P(Y = 1|x)}{1 – P(Y = 1|x)} = w \cdot x \] 这就是说,在逻辑斯谛回归模型中,输出 \( Y = 1 \) 的对数几率是输入 \( x \) 的线性函数。或者说,输出 \( Y = 1 \) 的对数几率是由输入 \( x \) 的线性函数表示的模型,即逻辑斯谛回归模型。
模型参数估计-极大似然估计
这样就变为对数似然函数为目标函数的最优化问题
似然函数(Likelihood Function)的作用是 量化参数(如模型权重 ww)对观测数据(训练样本)的拟合程度,并通过最大化似然函数来找到最优参数


为了简化计算(将连乘转化为求和),对似然函数取自然对数得到对数似然函数

•目标:求出使这一对数似然函数(逻辑回归损失函数)的值最大的参数w1,w2,…,wn,使得L(w)取得最大值。
总结:

线性回归,感知机,逻辑回归