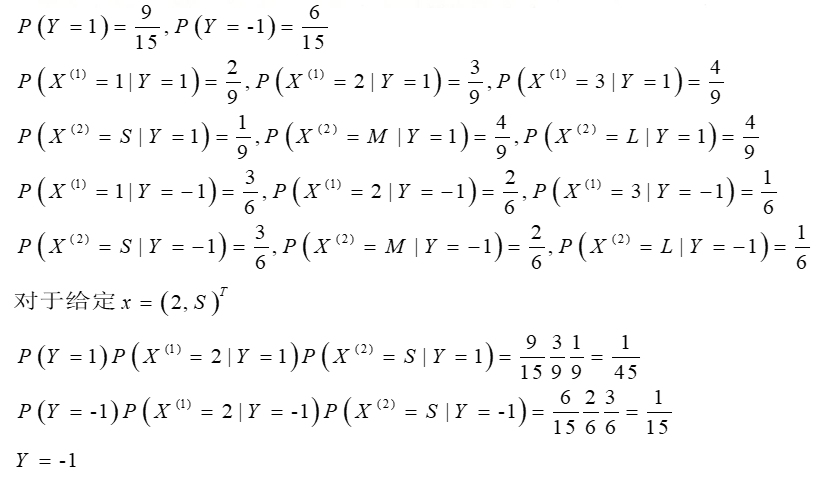条件概率 / 全概率公式

$$ P(B|A) = \frac{P(A \cap B)}{P(A)} $$

$$P(A \cap B) = P(A) \times P(B|A)$$

贝叶斯公式

$$P(A|B) = \frac{P(B|A)P(A)}{P(B)}$$

先验概率（Prior Probability）：
在未观察到新数据前，基于已有知识对事件概率的初始估计。
公式：P(假设)

似然概率（Likelihood）：
在假设成立的条件下，观察到当前数据的概率。
公式：P(数据∣假设)

后验概率（Posterior Probability）：
在观察到新数据后，对假设概率的更新结果。
公式：P(假设∣数据)

后验概率通过贝叶斯定理计算，似然概率用条件概率计算

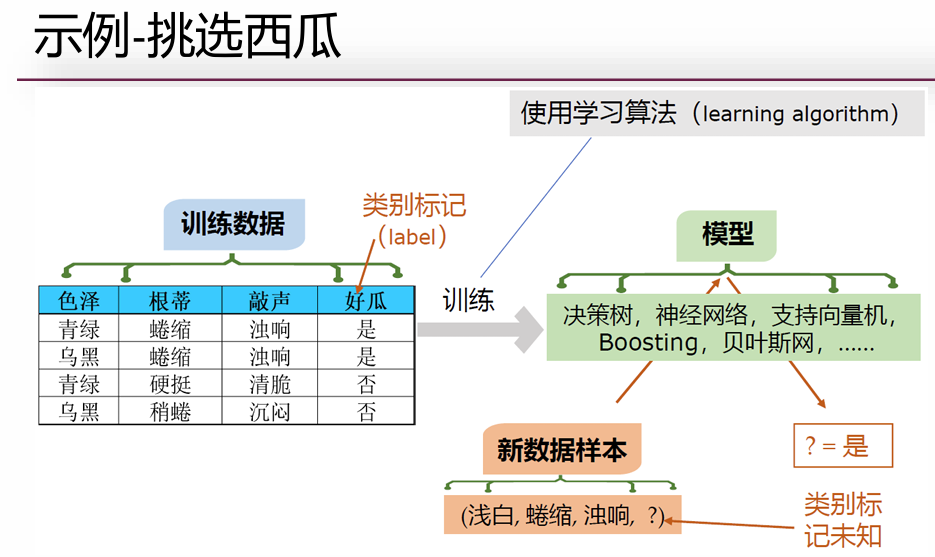
朴素贝叶斯分类模型

朴素贝叶斯方法是在贝叶斯算法的基础上进行了相应的简化，即假定给定目标值时属性之间相互条件独立。

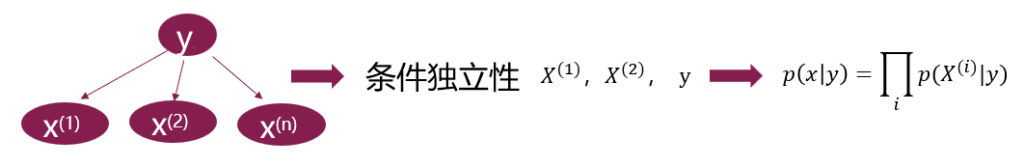
虽然这个简化方式在一定程度上降低了贝叶斯分类算法的分类效果，但是在实际的应用场景中，极大地简化了贝叶斯方法的复杂性。

贝叶斯分类是一类分类算法的总称，这类算法均以贝叶斯定理为基础，故统称为贝叶斯分类。而朴素贝叶斯（Naive Bayes）分类是贝叶斯分类中最简单，也是常见的一种分类方法。

目的：$$\arg\max p(y|x) = \arg \max\limits_{y\in\{0,1\}} \frac{p(x,y)}{p(x)} = \arg \max\limits_{y\in\{0,1\}} p(y)p(x|y)$$

目标是通过最大化后验概率 P(Y=y∣X=x)P(Y=y∣X=x) 来确定最优类别 y

去掉分母的原因：P(X=x) 的值仅依赖于输入 X=x，与当前比较的候选类别 y无关。无论我们算 P(Y=0∣X=x)还是 P(Y=1∣X=x)，分母 P(X=x)都是相同的，分类问题只需比较相对大小，无需计算绝对概率值。因此分母是冗余的。

其中 \( p(X) \) 是常数，先验概率 \( p(Y) \) 可以通过训练集中每类样本所占的比例进行估计。给定 \( Y=y \)，如果要估计测试样本 \( X \) 的分类，由朴素贝叶斯分类得到的后验概率为：

\[
p(Y = y|X) = \frac{p(Y = y)\prod\limits_{i=1}^{n}p(X^{(i)}|Y = y)}{p(X)}
\]
从计算分析中可见，\( p(X^{(i)}|Y) \) 的计算是模型关键的一步，这一步的计算视特征属性的不同也有不同的计算方法

• 对于离散型的特征属性 \( X^{(i)} \)，可以用类Y中的属性值等于 \( X^{(i)} \) 的样本比例来进行估计。
• 对于连续性的特征属性 \( X^{(i)} \)，通常先将 \( X^{(i)} \) 离散化，然后计算属于类$Y$的训练样本落在 \( X^{(i)} \) 对应离散区间的比例估计 \( p(X^{(i)}|Y) \)。也可以假设 \( p(X^{(i)}|Y) \) 的概率分布，如正态分布，然后用训练样本估计其中的参数。
• 而在 \( p(X^{(i)}|Y) = 0 \) 的时候，该概率与其他概率相乘的时候会把其它概率覆盖，因此需要引入Laplace修正。做法是对所有类别下的划分计数都加一，从而避免了等于零的情况出现，并且在训练集较大时，修正对先验的影响也会降低到可以忽略不计

流程

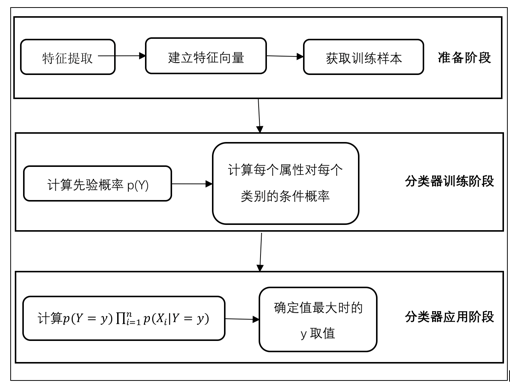
例题

例2：