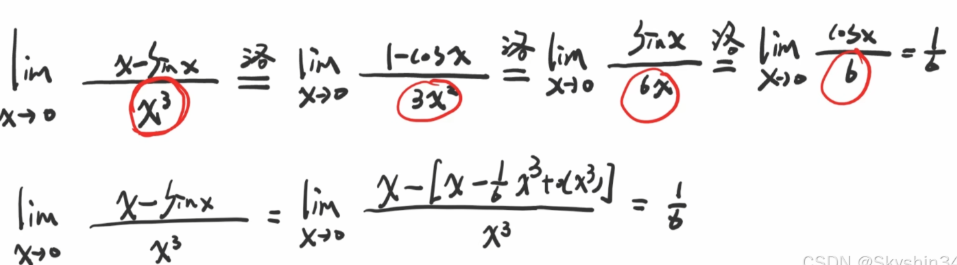参数方程和参数曲线的定义:
假设 \( x \) 和 \( y \) 都由第三个变量 \( t \)(称为参数)通过以下方程给出:\(\)
\[x = f(t) \quad y = g(t)\]
(称为参数方程)。每个 \( t \) 的值确定一个点 \((x, y)\)。随着 \( t \) 的变化,点 \((x, y) = (f(t), g(t))\) 也会变化并描绘出一条曲线 \( C \),我们称之为参数曲线。
FAMILIES OF PARAMETRIC CURVES 参数曲线族
研究以下参数方程定义的曲线族:\[x = a + \cos t\] \[y = a \tan t + \sin t\]

当 a<−1时,两支曲线都是光滑的;但当 a达到 −1时,右支曲线出现一个尖锐点sharp point,称为尖点cusp。对于 a 在 −1 和0之间,尖点变成一个环,随着 a 接近0,环变大。当 a=0 时,两支曲线合并形成一个圆。对于 a 在0和1之间,左支曲线有一个环,当 a=1 时,环缩小为尖点。对于 a>1,两支曲线再次变得光滑,并且随着 a 进一步增加,曲率减小。
作业完成记录:
Visual Studio 中的 Python 教程步骤 5,安装包 | Microsoft Learn
按照上面的步骤在VS中导入Python的matplotlib库
from math import radians
import numpy as np
import matplotlib.pyplot as plt
# 设置参数范围
a_values = np.arange(-5, 5.5, 0.5) # a从-5到5,步长0.5
t = np.linspace(-2*np.pi, 2*np.pi, 1000) # t从-2π到2π
plt.figure(figsize=(10, 8))
for a in a_values:
# 计算x和y值
x = a + np.cos(t)
y = a * np.tan(t) + np.sin(t)
# 处理奇点(tan(t)的无穷大点)
# 找到cos(t)接近0的点(即tan(t)接近无穷大的点)
mask = np.abs(np.cos(t)) > 0.01 # 忽略cos(t)接近0的点
# 绘制曲线
plt.plot(x[mask], y[mask], label=f'a={a:.1f}')
# 美化图形
plt.title('Family of Curves: x = a + cos(t), y = a*tan(t) + sin(t)')
plt.xlabel('x')
plt.ylabel('y')
plt.grid(True)
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)
plt.xlim(-10, 10) # 根据需要调整
plt.ylim(-20, 20) # 根据需要调整
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left') # 将图例放在图外右侧
plt.tight_layout()
plt.show()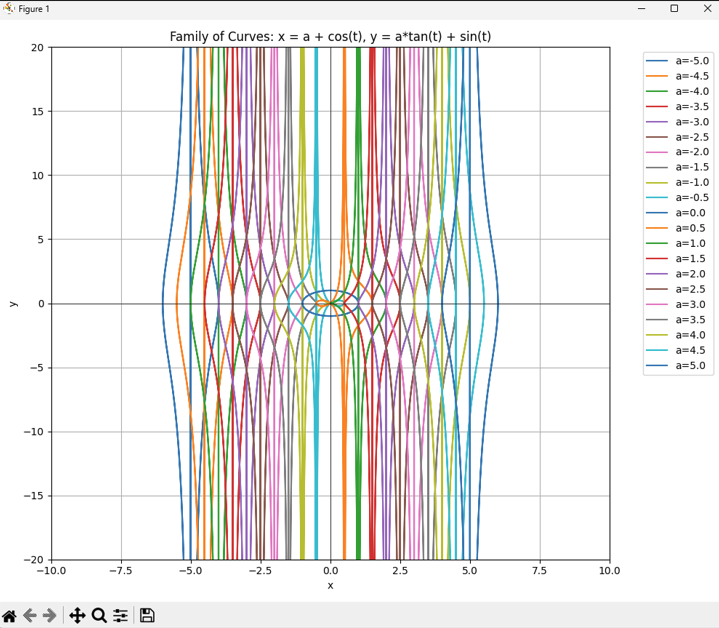
Aec Length 弧长
圆的弧长 – 圆弧
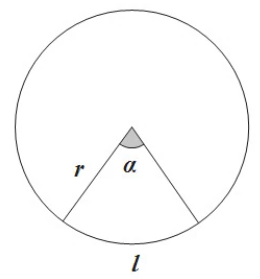
\[l = \alpha r\] 角为弧度制表示角的单位写作rad
一般光滑曲线的弧长公式
由平面直角坐标得到的弧长公式
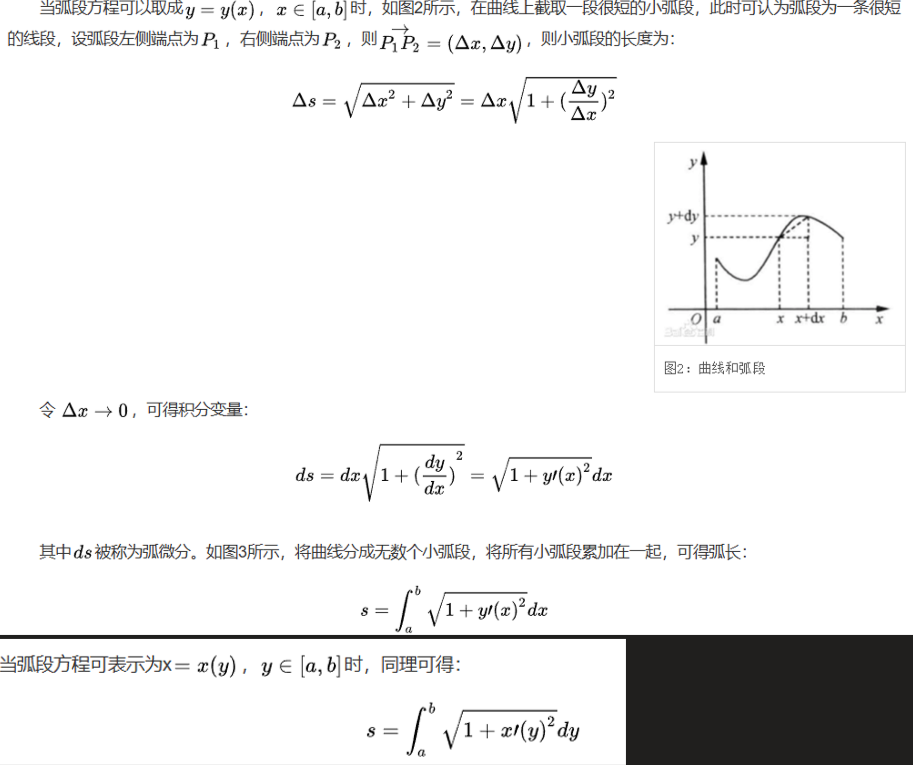
但该弧长计算方法只能计算形如 \( y = y(x) \),\( x \in [a, b] \) 或者 \( x = x(y) \),\( y \in [a, b] \) 的曲线。当计算形如圆、螺线、双纽线等曲线弧长时,由于曲线可能出现“回转”,\( y'(x) \) 或 \( x'(y) \) 回转处会发散到无穷大。为了解决这个问题,可以将曲线先分割成若干段可以表示成函数形式的曲线,再分别进行计算。此外,有的曲线在直角坐标系中的表达式非常复杂,它的参数方程却非常简洁,这时不妨采用参数方程进行计算。
由参数方程得到的弧长公式
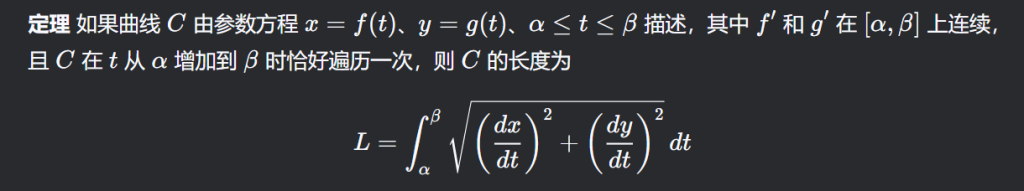
证明:



例题:

POLAR COORDINATES 极坐标
表示方法
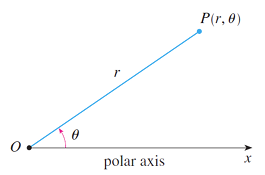
P 是平面中的任意其他点,设 r为从 O到 P 的距离,θ为极轴与直线 OP之间的角度(通常以弧度为单位),点 P 由有序对 (r,θ)表示,r和 θ称为 P的极坐标。规定
- 角度为+代表从极轴逆时针方向,-代表顺时针方向旋转
- 如果 \(r > 0\),点 \((r, \theta)\) 位于 \(\theta\) 所在的象限;如果 \(r < 0\),则位于极点的相反象限。注意,\((-r, \theta)\) 表示的点与 \((r, \theta + \pi)\) 相同。
- 如果 P=O,则 r=0,并且我们约定 (0,θ)对任意 θ 值都表示极点。


极坐标与Cartesian坐标相互转换
已知极坐标
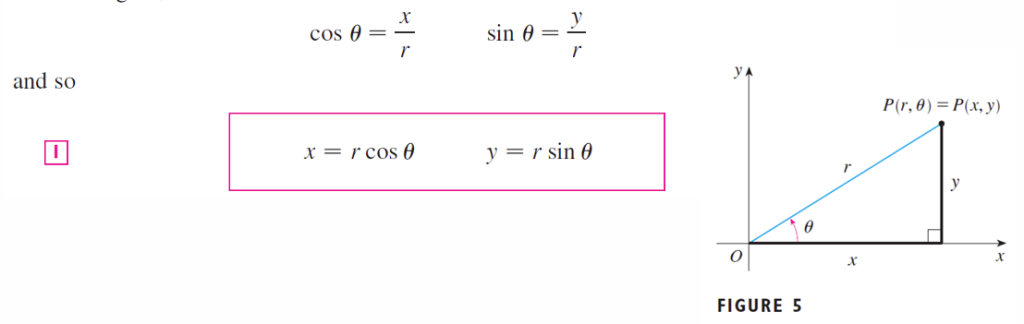
已知笛卡尔坐标
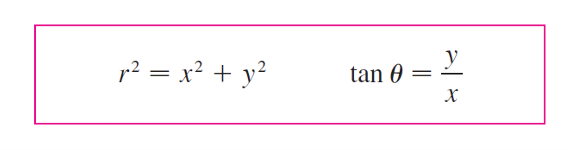
- 如果X/Y =0,画图就可知道角度,不用再计算了
如果用tan的方式计算从笛卡尔到极坐标的角度转换,先画图判断笛卡尔表示下点(之前是复数)在第几象限,因为tan的周期是Π,对于角度不同的角,结果是一样的,要根据实际角度,加减Π调整结果




POLAR CURVES 极坐标曲线
极坐标方程 r=f(θ)或更一般地 F(r,θ)=0的图形由所有至少有一个极坐标表示 (r,θ)满足方程的点 P组成