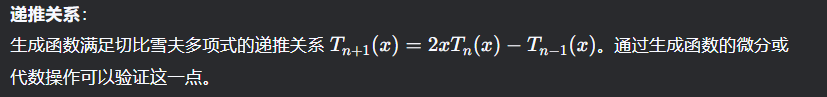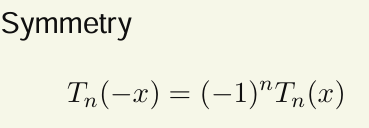了解算法 – Skyshin34的博客

本文最后更新于0 天前，其中的信息可能已经过时，如有错误请留言

前言：那些群星闪耀的算法

2016年Nick Higham更新列表

牛顿法和拟牛顿法；
矩阵分解（LU、Cholesky、QR）；
奇异值分解SingularValueDecomposition（SVD）、QR和QZ算法；
蒙特卡洛方法 Monte Carlo method；
快速傅里叶变换；
克雷洛夫子空间迭代法；Krylov Subspace Iteration
JPEG；
PageRank；
线性规划的单纯形法；
卡尔曼滤波器 Kalmanfilter

当今视角

PageRank算法
快速傅里叶变换（FFT）
RSA算法（1977年）
Dijkstra算法（1956年）
K均值聚类算法（1967年）
支持向量机（SVM）（1990年代）
期望最大化（EM）算法（1970年代）
霍夫曼编码算法（1950年代）
Bellman-Ford算法（1950年代）
Levenshtein距离算法（1960年代）

新兴趋势

深度学习算法
量子算法
强化学习算法
区块链算法
可解释AI算法
联邦学习算法
元启发式算法

JPEG算法

基于离散余弦变换（DCT）的有损压缩形式将视频源的每一帧/场从空间（2D）域转换到频率域（也称为变换域）

基于人类心理视觉系统的感知模型会丢弃高频信息，例如强度的急剧变化和色调。

在变换域中，减少信息的过程称为量化。变换域是图像的便捷表示，因为高频系数对整体图像的贡献较小，通常为小值且具有高压缩性。

简单来说，量化是一种将大数值范围（每个数字出现频率不同）优化缩小为较小范围的方法。量化后的系数随后被序列化并无损打包到输出比特流中。

Order notation 阶符号 -表达算法复杂度

讨论算法(函数)的复杂度时，通常不关心具体操作次数，而只关注“阶” \( O(n^\alpha) \)即仅最高幂次重要，低次幂甚至最高幂的系数也不重要。

用于描述函数在自变量趋向于特定值或无穷大时函数的增长率的上限。有相同渐近增长率的不同函数可以用相同的 O 符号表示。所以其代表的是一个集合而不是一个数，比如某个算法（函数）的复杂度是O(n^3)，意味着这个算法的时间复杂度属于增长率不超过n^3次方多项式的函数集合。正式定义为：

如果存在一个正常数M和某个整数a(通常是0或无限) ，使得对于所有 \( x \geq \delta\)，函数 \( f_n \) 的绝对值不超过 M 倍 \( g_n \) 的绝对值

也可写成极限的形式(做题常用)，如果进一步极限的值为0则将大O改写为小O

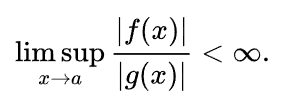
如果将定义中的≤改为＜则为小o的定义

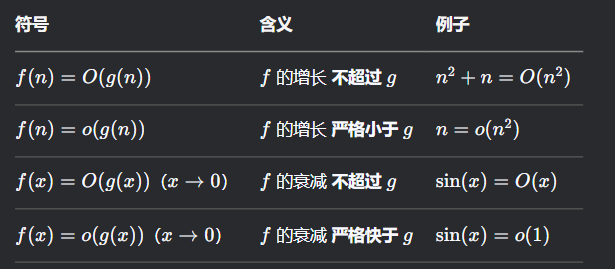
例题

用定义证明时，虽然右侧设的函数只要大于左侧即可，但一般将所有项保留系数，参数改为最高次项，所以上面设为3n^4，这样做的好处是n可以取任意正数，如果设为其他的函数需要找对应的n>n0的n0

这背后是遵循，选择距左侧函数最近的上限，所有的上限都可以写进O()中，但一般写最近的函数，比如如上例中O(n^4)，则幂大于4的n项都可以作为上限，但是我们通常不应该这样写，但也不能算错

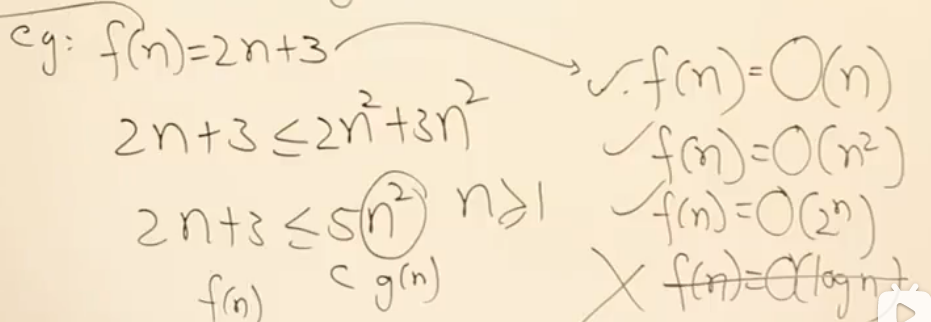
例2：

补充: 函数的/(omega/) 下限记号和 /(/theta/ 平均界限记号

如果不确定某个函数属于哪个，一般就表示为这个函数的上限

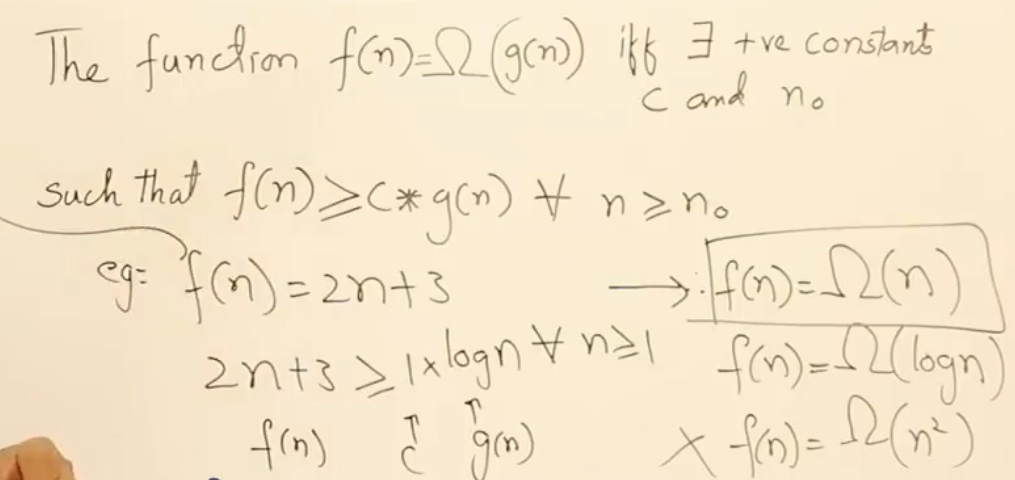
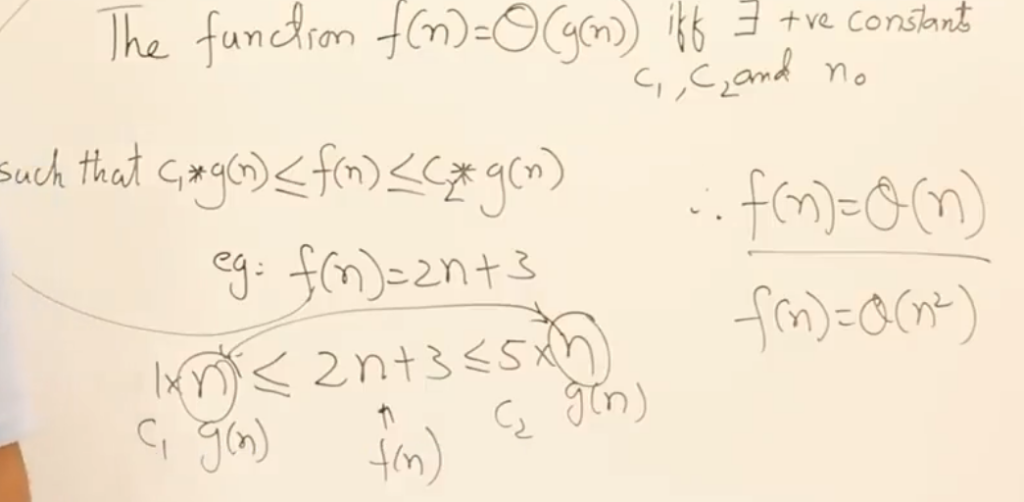
平均界限的上限O()和下限\(\omega\)中的变量必须相同，如果修改上限，下限也会跟着改变从而导致错误。所以平均界限不像上下限一样有很多符合条件的情况，结果是唯一的

不要将上下限与算法中的最佳和最坏情况混淆（目前还无法理解）

拓展：为何降低算法复杂度如此重要

可以通过以下一个例子直观感受：计算复杂度只增加了10^3个量级，对于计算机这种高速计算的机器，从这个过程也可以看出性能越好的机器越能推迟复杂度所带来的缺陷的时间，比如现在有一个每秒执行1百亿次的电脑，对于复杂度为1000只能从1s缩小为0.1s，之减少了0.9s。而对于n=1000000可以从10^9缩小为10^8(基数大)

我们可以通过以下的方式尽可能缩小计算时间，但是通过硬件提升的想法近些年已经到达了一个瓶颈，所以我们必须不断探寻复杂度更低的算法

从代码的角度理解大O表示法

Refrence：算法复杂度分析，一篇就够了_所提出方法的复杂度怎么分析-CSDN博客

public void print(int n){
    int a = 1; //执行1次
    for(int i=0;i<n;i++){//执行n次
        System.out.println(a+i); //执行n次
    }
}

复杂度计算规则

顺序执行的代码：复杂度相加（用 +）。
嵌套的循环：复杂度相乘（用 ×）。

假设我们执行一行代码平均需要用的是一个常数 \( t = \text{unit\_time} \)，那计算上面代码（算法）的用时，就是执行总行数乘以 \(\text{unit\_time}\)。上面的代码总时间就是：\[T(n) = (1 + 2n)\text{unit\_time}\]
其中n是方法参数，代表算法的数据规模。可以看出，执行用时和(1+2n)成正比。我们用大O表示法表示该算法的时间复杂度\( O \) 就是：\[O(1 + 2n)\]
大O表示法会忽略常量、低阶和系数，所以记作：\[O(n)\]
大O表示法描述的是随着数据规模增长时，算法的增长变化趋势。并不代表实际的执行时间，并不代表实际的执行时间，并不代表实际的执行时间，并不代表实际的执行时间。可以通过数据量从1变为n时，假设原来执行一次需要t时间，现在所需要的时间t’。t’ / t的结果即为O。比如标量积只需要1次乘法，如果一次乘法所需t时间。n个数据的点积就需要n次乘法，时间为nt。nt/t =n。所以时间复杂度为O(n)

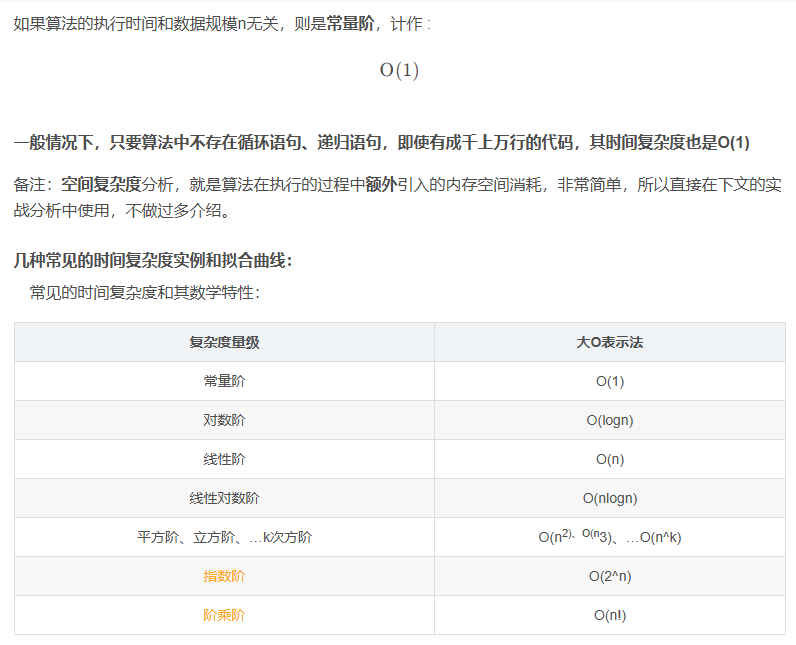
如果算法的执行时间和数据规模n无关，则是常量阶，记作：
\[ O(1) \]
一般情况下，只要算法中不存在循环语句、递归语句，即使有成千上万行的代码，其时间复杂度也是O(1)。比如：因为计算时间不随数据量的变化而变化

几种常见的时间复杂度实例和拟合曲线：

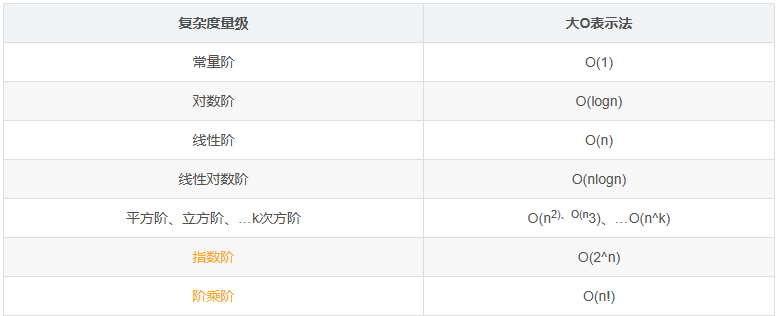
常见的时间复杂度和其数学特性：

代数方法简化问题降低复杂度

交换求和顺序，将双重求和拆分为两个独立的单重求和

没拆分之前，需要 \(n^2\)次乘法和 \(n^2 -1\) 次加法，总时间复杂度为：\(O(n)×O(n)×O(1)=O(n^2)\)

def double_sum_naive(a, b):
n = len(a)
result = 0
for i in range(n): # O(n)
  for j in range(n): # O(n)
     result += a[i] * b[j] # O(1)
return result

分离后，总时间复杂度：O(n) + O(n) = O(n)

def double_sum_optimized(a, b):
sum_a = sum(a) # O(n)
sum_b = sum(b) # O(n)
return sum_a * sum_b # O(1)

同理有：

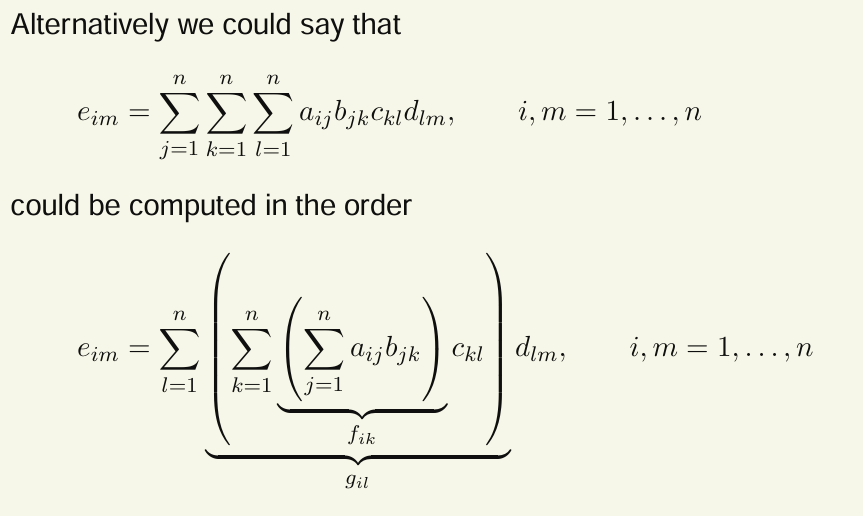
外积

外积（英语：Outer product），在线性代数中一般指两个向量的张量积，其结果为一矩阵；与外积相对，两向量的内积结果为标量。

矩阵乘法分解为向量内积运算和向量数乘

Fibonacci numbers斐波那契数列通过迭代存储中间结果避免重复计算

//递归实现
function F = Fibol(n)
    if n == 0
        F = 0;
    elseif n == 1
        F = 1;
    else
        F = Fibol(n-1) + Fibol(n-2);
    end
end

每次调用 Fibol(n) 会递归调用 Fibol(n-1) 和 Fibol(n-2)，导致相同的子问题被多次计算。递归调用的次数呈二叉树形式增长，总节点数约为 \(2^n\)，因此时间复杂度为 \(O(2^n)\)

//迭代实现
function F = Fibo2(n)
    FA = [0, 1];
    for i = 3:n+1
        FA(i) = FA(i-1) + FA(i-2);
    end
    F = FA(n+1);
end

复杂度为线性O(n)。通过迭代和存储中间结果(所以牺牲了空间复杂度)，避免了重复计算，显著提升效率。

多项式的不同表示方法

霍纳法则（horner’s rule)—计算多项式值的高效算法

霍纳法则 – 知乎

对于多项式求值问题，我们最容易想到的算法是求出每一项的值然后把所求的值累加起来，这种算法的时间和空间效率都不高。霍纳法则通过将多项式重新分解为嵌套的线性形式，减少计算复杂度。

其实上面的题主最后并没有给出这种方法可以简化多项式计算的的理由，其实是将高次幂转化为连续的线性乘法，从而避免直接计算高次幂，从而减少了一层循环

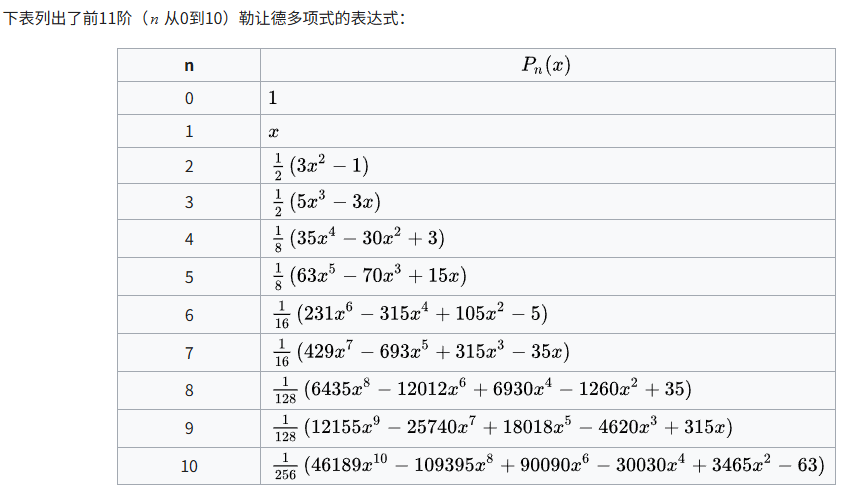
Legendre basis 勒让德多项式

是一组在数学和物理学中非常重要的正交多项式，它们的递推关系提供了一种高效的计算方法，可以避免直接求解微分方程或积分表达式。

切比雪夫多项式到单项式（Chebyshev to Monomials）

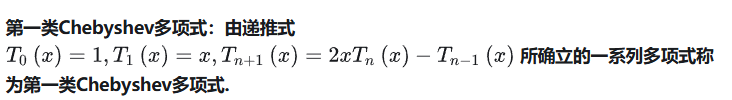
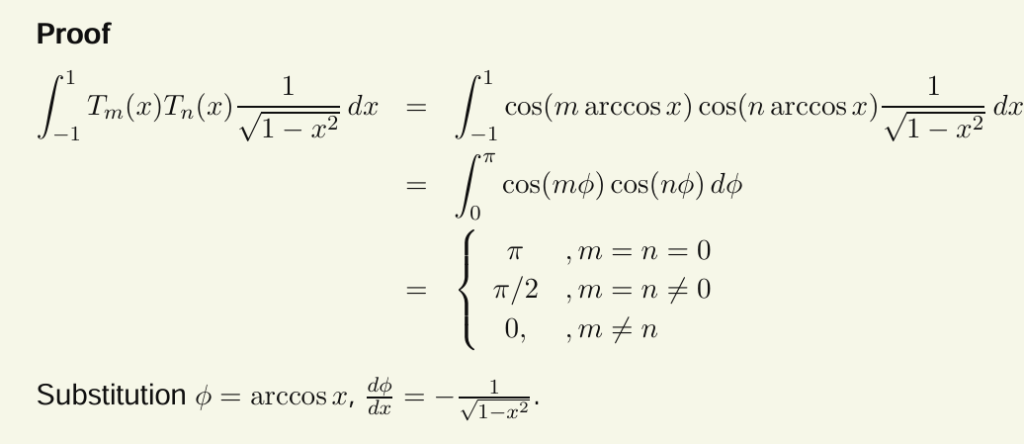
性质

生成函数的核心思想是将一个数列（这里是 {Tn(x)}编码为一个形式幂级数。通过操作生成函数，可以得到指定的切比雪夫多项式中的某个单项