Reference：

11.2 齐次线性方程组的基础解系和通解 – 知乎

线性方程组解的判定

\[A\vec{x}=\vec{b}\]若无解，当且仅当:系数矩阵的秩数 < 增广矩阵的秩数

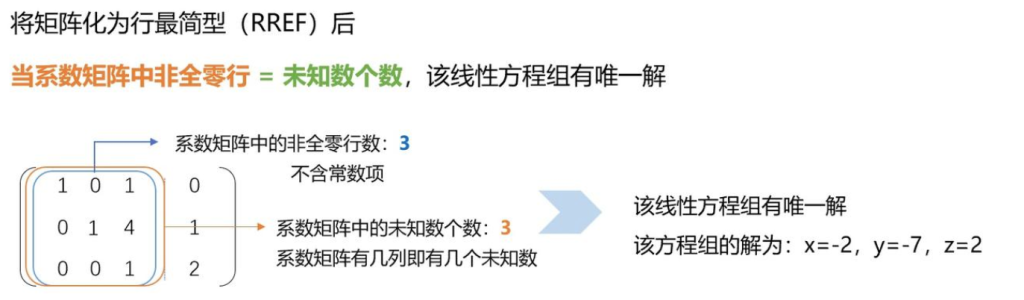
\[A\vec{x}=\vec{b}\]有唯一解当且仅当：系数矩阵的秩数 = 未知数个数

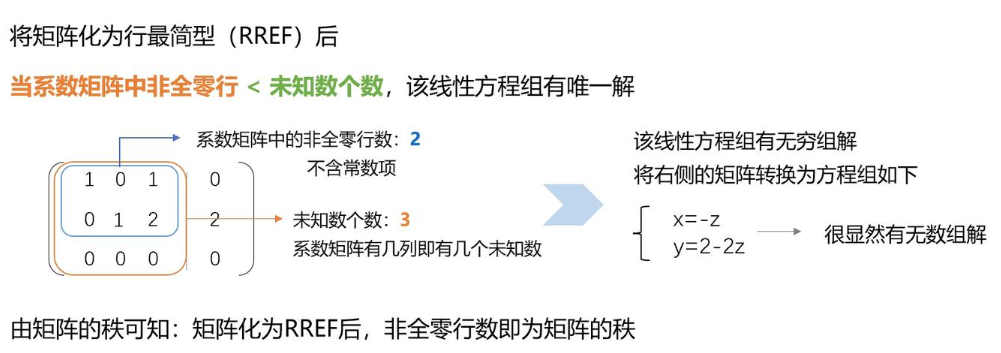
\[A\vec{x}=\vec{b}\]有无穷多组解当且仅当：系数矩阵的秩数 < 未知数个数

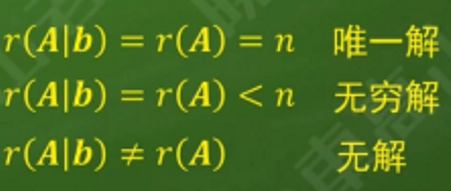
 齐次线性方程组解的判定

齐次线性方程组，因为等号右边全为零，所以不会存在无解的情况

至少存在一组全零解，使得等式成立

所以齐次线性方程组的解只有两种情况：

① 有唯一解（系数矩阵的秩数 = 未知数个数），即为零解

② 有无穷多组解（系数矩阵的秩数 < 未知数个数），即为无穷多组解

那齐次线性方程组的无穷多组解，该如何表示出来呢？

答案是：用基础解系来表达这无穷多组解

基础解系(极大线性无关组)

指在无穷多组解中，找到一组解，且满足：

① 这组解内的向量线性无关

② 方程组的任意一个解都可由这组向量线性表示

那么这组解（向量组），就称为基础解系

这和极大线性无关组是一回事

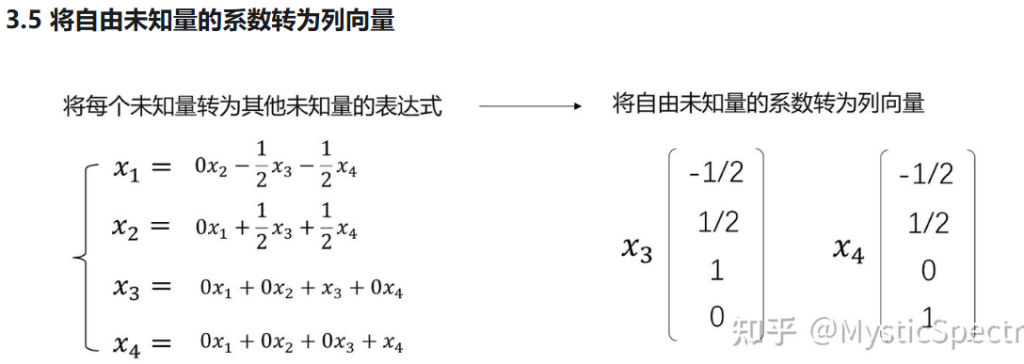
基础解系到通解

通解就是线性方程组解的具体表达方式有了基础解系（一组线性无关的列向量）

那么每个列向量×对应系数再相加即为该方程组的通解，对应系数可为任意常数

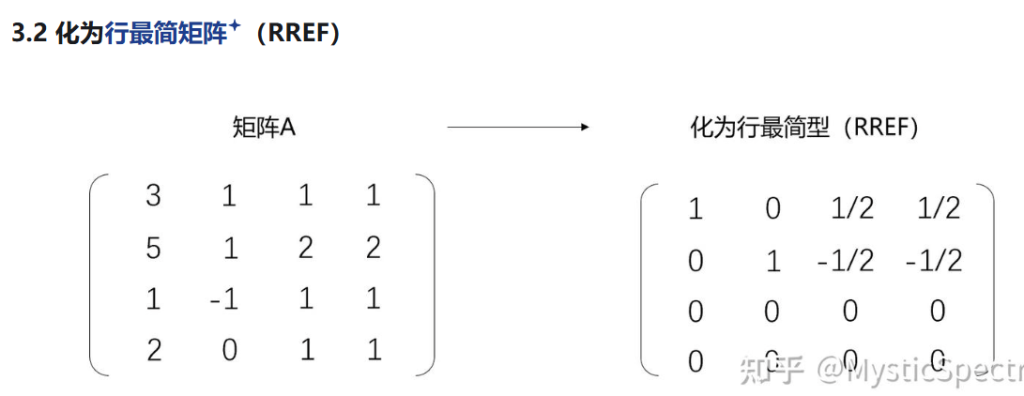
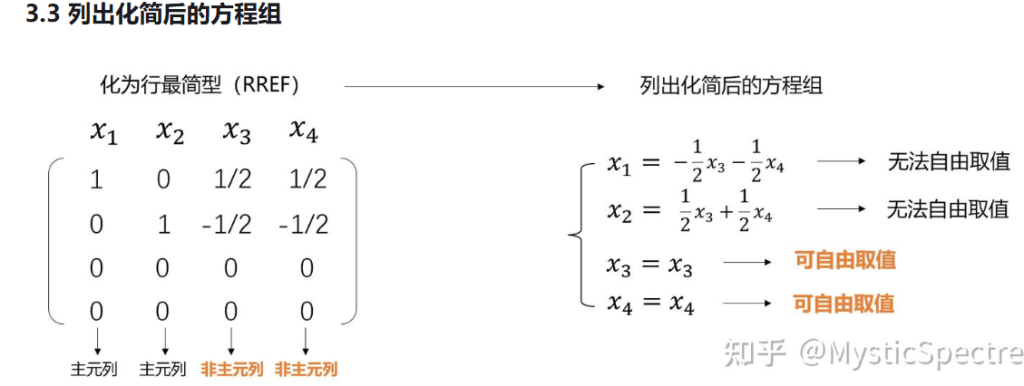
求解齐次线性方程组的基础解系和通解

非齐次线性方程组

非齐次线性方程组的通解由齐次的通解和非齐次的特解组成

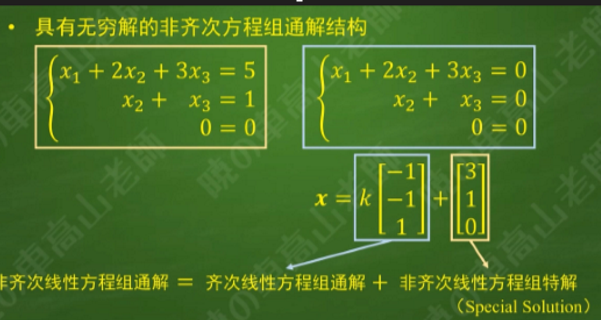
在阶梯增广矩阵中令全体自由变量为0即可得到特解。